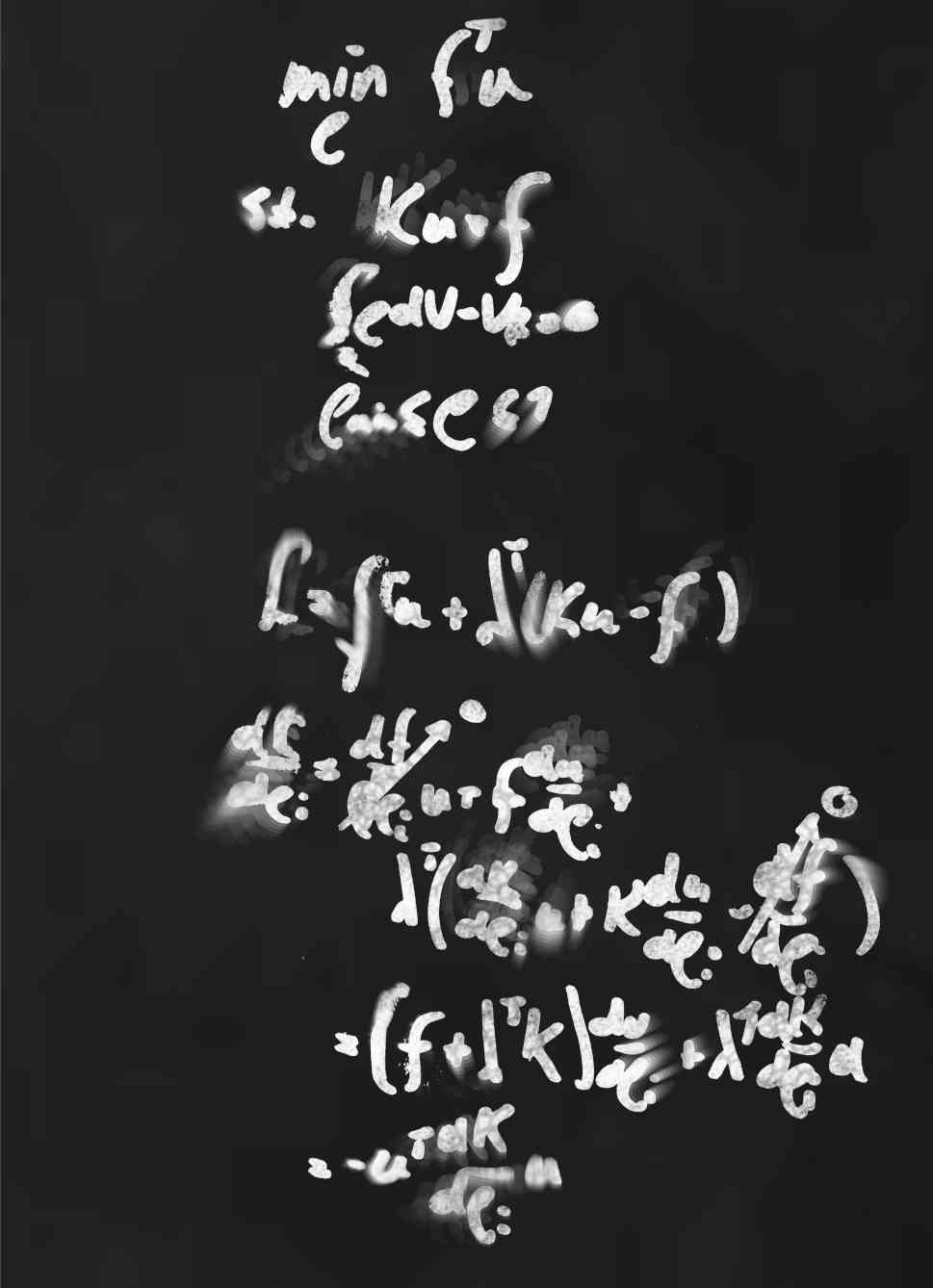Research
The main body of my PhD was the development of a method to include additive manufacturing constraints into topology optimization in a practical, efficient manner. This resulted in four research papers, linked below.
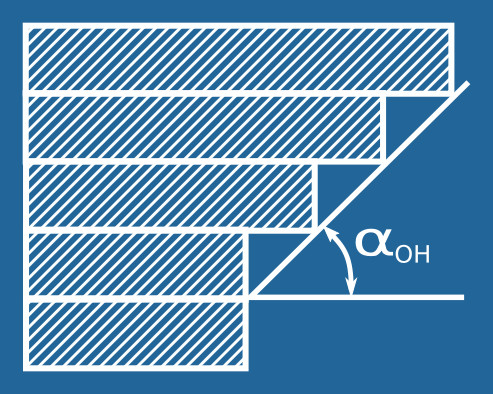
The additive manufacturing constraint considered was the overhang consraint: each layer that is printed has to have some support from the previous layer, which limits the distance it can expand with respect to the previous layer. The maximum expansion rate is measured with the so called overhang angle αOH:
The highlights shown on the remainder of this page are only those simulations that also resulted in a nice visual. For more information on the research or the examples, contact me at
The overhang constraint can have a large influence on the design, as can be seen in the figure below where the overhang angle is gradually increased:


Paper 1

Paper 2

Paper 3

Paper 4
Gripper mechanism
Goal: design a gripper mechanism that closes when the bottom is pushed. Using symmetry, a quarter of the domain is simulated. It is meshed with 1.5 million nodes, and solved on 40 CPUs.
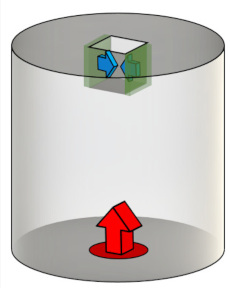
Optimziation problem.
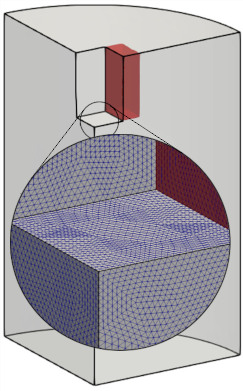
Simulation domain.
Optimization process.
Action of two gripper designs.
Crane hook optimization
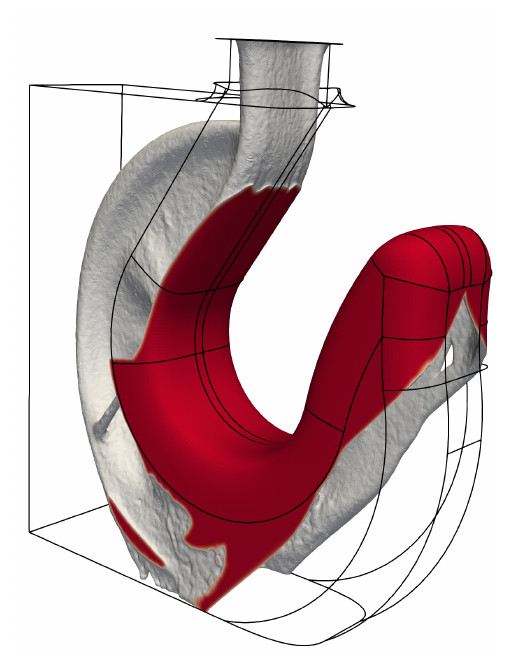
Goal: optimize a crane hook such that it can be manufactured with additive manufacturing. The resulting design is printable without support structures. During the optimization a bug was encountered, and the debugging process resulted in a nice visual displayed on the right.
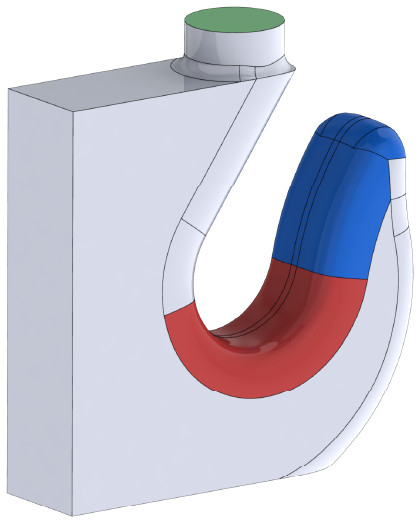
Design domain. Vertical load is applied to red area, green area is fixed.
Optimized design.
Visualization of back propagation through the domain.
Cake server optimization
Our professor promised to bring cake when an optimization above 100 million degrees of freedom was performed. It seemed fitting to optimize a cake server: the handle is fixed and a load is applied on the blade, imitating a piece of cake. The detail in the final design is astonishing. Two "wings" appear on both sides of the handle to counter the torque induced by the piece of cake. The optimization was performed on an unstructured mesh, and took 14 hours on 280 CPUs.
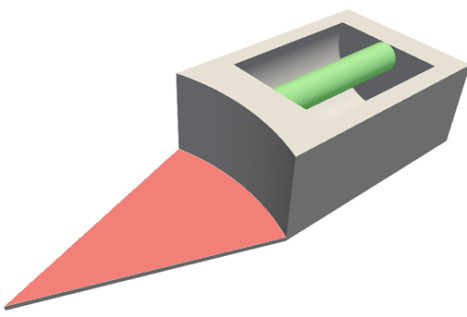
Design domain.

Optimized design.

Optimized design rendered.
Stool optimization
This optimization was performed to test a new optimization code. Instead of using unstructured meshes, the optimization code was aimed at structured grids and fully exploits all the benefits of it. As a result, this optimization can be run on a single desktop, with the use of a matrix-free solver.
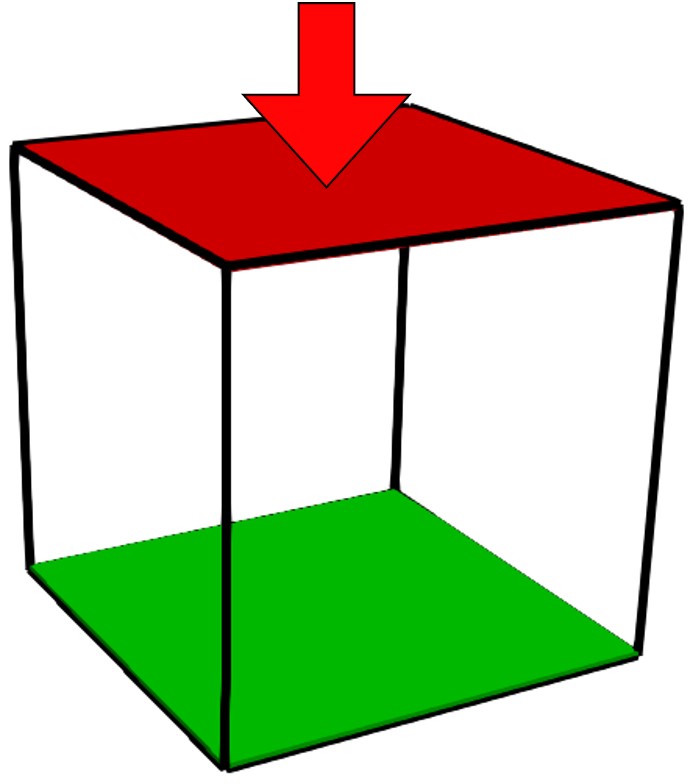
Design domain. Vertical load is applied to red area, green area is fixed.
Optimization process.